O level Geometrical Construction Quiz 1
15 QuestionsQuiz Description
Made up of 15 questions of which each question has four options with just one correct answer, o level geometrical construction quiz 1 has been set based on the national curriculum for the ordinary level. After successfully going through these questions, answering gce geometrical construction questions will just be a piece of cake for you.
Geometrical construction simply refers to the process by which lines, angles and so many other geometric shapes and figures use only a compass and a ruler. It is important to note that geometrical construction is done without the use of specific measurement of angles and lengths.
It is mostly used for
- Finding the midpoint of a segment.
- Constructing the perpendicular bisector from a segment.
- Drawing a perpendicular line from a point to a line.
- Bisecting an angle.
With gcequiz.com revising and better preparing for your end of year exams has been made easy plus Past ordinary level gce questions that have been made available just for you.
Good Luck
To divide a line segment AB in the ratio 3:4, first, a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is:
To divide a line segment AB of length 7.6cm in the ratio 5:8, a ray AX is drawn first such that ∠BAX forms an acute angle and then points A1, A2, A3, ….are located at equal distances on the ray AX and the point B is joined to:
To construct a triangle similar to a given ΔPQR with its sides 5/8 of the similar sides of ΔPQR, draw a ray QX such that ∠QRX is an acute angle and X lies on the opposite side of P with respect to QR. Then locate points Q1, Q2, Q3, … on QX at equal distances, and the next step is to join:
To construct a triangle similar to a given ΔPQR with its sides, 9/5 of the corresponding sides of ΔPQR draw a ray QX such that ∠QRX is an acute angle and X is on the opposite side of P with respect to QR. The minimum number of points to be located at equal distances on ray QX is:
To construct a pair of tangents to a circle at an angle of 60° to each other, it is needed to draw tangents at endpoints of those two radii of the circle, the angle between them should be:
To divide a line segment PQ in the ratio m:n, where m and n are two positive integers, draw a ray PX so that ∠PQX is an acute angle and then mark points on ray PX at equal distances such that the minimum number of these points is:
To draw a pair of tangents to a circle which are inclined to each other at an angle of 45°, it is required to draw tangents at the endpoints of those two radii of the circle, the angle between which is:
A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of ___________ from the centre.
To construct a triangle ABC and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle. A ray AX is drawn where multiple points at equal distances are located. The last point to which point B will meet the ray AX will be:
To construct a triangle similar to a given ΔPQR with its sides 3/7 of the similar sides of ΔPQR, draw a ray QX such that ∠QRX is an acute angle and X lies on the opposite side of P with respect to QR. Then locate points Q1, Q2, Q3, … on QX at equal distances, and the next step is to join:
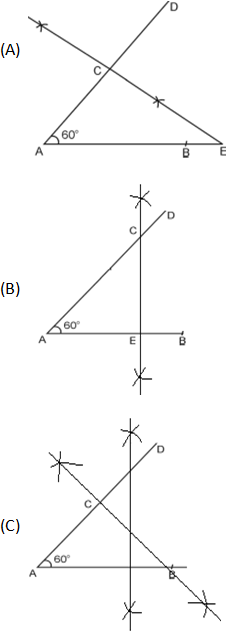
Draw the line segment AB = 5 cm. From the point A draw a line segment AD = 6cm making an angle of 60 degrees with AB. Draw a perpendicular bisector of AD. Select the correct figure.
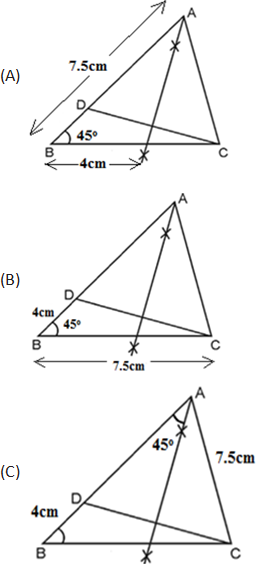
For ∆ABC in which BC = 7.5 cm, ∠B =45 degrees and AB – AC = 4, select the correct figure.
To divide a line segment AB in the ratio 5:6, draw a ray AX such that ∠BAX is an acute angle, then drawa ray BY parallel to AX and the points A1, A2, A3,…. and B1, B2, B3,…. are located to equal distances on ray AX and BY, respectively. Then, the points joined are
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°, it is required to draw tangents at the end points of those two radii of the circle, the angle between which is:
To divide a line segment AB in the ratio 5:7, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is:


